Lisa Piccirillo ’13.
Photos: Kelly Davidson
A Tough Knot to Crack
[Editor’s note: A version of this article first appeared in the Boston Globe Sunday Magazine.]
Half a century ago, a brilliant young mathematician named John Horton Conway discovered, of all things, a knot. This wasn’t the sort of knot that you’d be likely to encounter in the real world. You could certainly create it out of string if you wanted to, but generally speaking, it existed only in Conway’s calculations. There are thousands upon thousands of these kinds of conceptual tangles in a bewildering corner of mathematics known as knot theory, but even there Conway’s discovery was special—not so much for what it was, but for what it might or might not be. Yes, that is confusing, but when talking knot theory, it’s best to accept that things tend to get a little fuzzy.
In any case, Conway’s knot was hardly remarkable at first glance. With just eleven crossings, or places where it overlapped itself, it was rather nondescript by the standards of higher-dimensional knot theory. But the knot had one property that made it the subject of intense mathematical scrutiny. Conway, who died recently at age 82 of complications from COVID-19, made innumerable contributions to the field of mathematics, yet it was his knot that specialists would return to again and again. And again and again, these decorated mathematicians were unable to find a solution to what became known as the Conway knot problem.
The problem had to do with proving whether Conway’s knot was something called “slice,” an important concept in knot theory that we’ll get to a little later. Of all the many thousands of knots with twelve or fewer crossings, mathematicians had been able to determine the sliceness of all but one: the Conway knot. For more than fifty years, the knot stubbornly resisted every attempt to untangle its secret, along the way achieving a kind of mythical status. A sculpture of it even adorns a gate at Cambridge University’s Isaac Newton Institute for Mathematical Sciences.
Then, two years ago, a little-known graduate student, and BC alum, named Lisa Piccirillo learned about the knot problem while attending a math conference. A speaker mentioned the Conway knot during a discussion about the challenges of studying knot theory. “For example,” the speaker said, “we still don't know whether this eleven crossing knot is slice.”
That’s ridiculous, Piccirillo thought to herself while she listened. This is 2018. We should be able to do that. A week later, she produced a proof that stunned the math world.

KNOT THEORY IS A SUBSPECIALTY of a field of mathematics known as topology, which is concerned with the study of spaces. What’s it used for? “The answer one memorizes is that topology is useful for understanding DNA and protein folding,” Piccirillo told me a few months ago as we sat—wearing masks and maintaining a good ten feet of distance—in an outdoor courtyard not far from where she lives in Cambridge, Massachusetts. “Apparently these things are very long and they like to stick to themselves, so they get all knotted up, and topology contains knot theory.”
When topologists think of knots, however, they don’t imagine them as you and I might: a length of rope with a gnarled twist or two in the middle. To them, a knot is more like an extension cord in which the two ends have been plugged together and the whole thing has been tossed onto the floor in a mess of crisscrosses. It’s essentially a closed loop with various places where the loop crosses over itself.
Now, let’s take one of these knots and think for a moment about the space in which it exists. To a topologist a knot is actually a kind of sphere. Topologists, in fact, see spheres everywhere. To them, a circle is a one-dimensional sphere, while the skin surrounding an orange is a two-dimensional sphere. And here is where minds tend to get blown: If we were to take that whole orange and glue it to another one, topologists would see the resulting object as a three-dimensional sphere, one that could be viewed as the skin of a four-dimensional orange. Don’t worry that you are unable to conjure such a higher-dimension image for yourself. Outside of a couple hundred experts, no one really can.
Piccirillo was already well on her way to joining the ranks of those couple hundred when, in the summer of 2018, a speaker at a math conference said something that would change the trajectory of her career. The speaker showed a slide depicting the Conway knot and explained that mathematicians had long suspected that the knot was not, in fact, slice, but no one had been able to prove it. So what does it mean for a knot to be slice? Let’s return for a moment to that four-dimensional orange. Inside of it there are disks—think of them as the surface of a plate. If a three-dimensional knot, like Conway’s, can bound such a disk, then the knot is slice. If it cannot, then it is not slice.
Topologists use mathematical tools called invariants to try to determine sliceness, but for half a century, these tools had been unable to help them prove the prevailing belief that the Conway knot wasn’t slice. Sitting in that lecture hall two years ago, however, Piccirillo sensed right away that the techniques she was using in a different area of topology might help the invariants solve the Conway knot problem. “I immediately knew that some work that I was doing for totally other reasons could at least try to answer this question,” she said. She started on the problem the very next day.


PICCIRILLO, WHO IS 29, grew up in Greenwood, Maine, which has a population of less than 900. She was an excellent student and her mother taught middle school math (her father was a welder and worked in sales), but there was little in her interests to suggest that she would become a world-class mathematician.
“I was an overachiever,” she told me. “I rode dressage. I was very active in the youth group at my church. I did drama. I was in band. I did everything.” Which is another way of saying that she wasn’t one of those math prodigies who’s programming computers and building algorithms at age four.
When Piccirillo arrived on campus for her first year at BC in 2009, she was as interested in subjects like theater as she was math. During a calculus class that year, though, she made a connection with Professor J. Elisenda Grigsby. “Lisa was in the very first class that I taught at BC,” Grigsby recalled. “It was not an advanced math course—probably more for people who are planning to major in science than ones who are planning on a career in mathematics.” Although Piccirillo lacked the polish of “gold-child mathematicians” who’ve been groomed since a young age, her creativity and intelligence stood out, and Grigsby took an interest in helping to develop her talent. “The people who typically get mentorship are the ones that fit the mold,” she said. “We're not just talking about men, we're talking about white men. I can't speak to how anyone else would have reacted to Lisa. All I know is that I do think that part of what drew me to her was a recognition that she was like me.”
“She really encouraged me,” Piccirillo said of Grigsby. “Eli really pushed me into trying another math class, and then liking the next class. I had already started on a progression.” Piccirillo then encountered another mentor at BC, Professor Joshua Greene. “That was fall 2011,” Greene recalled. “She was in the first class that I taught. I’ll never forget one of the exams. I printed it two-sided, and Lisa finished early. When I was reviewing the exams, I found that she had overlooked the back page. She was the only person who did that. She got the highest score in the class anyway. She was very talented.”
By fall of Piccirillo’s senior year, she was taking entry-level graduate courses. The following semester, she was on to more specialized graduate classes, which are known as topics courses. “To take a topics graduate course as an undergrad,” Greene said, “that was very special, very unusual.”
Piccirillo’s development as a mathematician during her time at Boston College was proof, more than anything else, of her own talent and commitment. But it spotlighted something else, too: an entire community of mentors, resources, and support systems that had been carefully designed by the math department several years before Piccirillo matriculated to BC, all with the express purpose of identifying and nurturing promising young mathematicians.
PROFESSOR SOLOMON FRIEDBERG came to Boston College in 1996, the first of a wave of impressive hires in the math department around that time. Over the next several years, Friedberg became convinced that the department needed to expand its offerings. At the time, the only math degree BC offered was a bachelor of arts. Solomon wanted to develop a Ph.D. program, and with it a bachelor of science degree for undergraduate students interested in the mathematical sciences.
The opportunity to make the case for such a program was the main reason that Friedberg agreed to become department chair in 2007. “During my first year as chair, we conducted a departmental self-study study,” he told me. “We understood that we would need to create a small Ph.D. program. BC wasn’t going to use a model where grad students do a lot of the teaching. That’s not our plan and that’s not our mission.” With that in mind, the department ultimately proposed a program that was centered on two broad areas, one being number theory and the other being the two closely related disciplines of geometry and topology. The proposal, as it happened, found receptive ears among University leadership.
Around this same time, BC was conducting a series of program reviews all across the university. “Cuberto Garza was the new provost during this review process, and, midway through, I stepped into the dean’s role in what is now the Morrissey College,” said David Quigley, who today is provost and dean of faculties. “Those program reviews led us to change directions in some areas, and scale back or close certain programs. But we were also able to identify some really promising emerging strengths on campus, including recognizing just what a jewel we had with the math department.”
When Friedberg made the department’s case for the new Ph.D. program, he emphasized his belief that it would benefit every math student at BC, undergrads and grads alike. “There’s a whole ecology of a math department,” he told me. New undergrads get to communicate and learn from more advanced undergraduates, who in turn get to interact with grad students while taking graduate-level courses. The graduate students, meanwhile, have access to the talent and experience of postdocs, who benefit from mentoring by faculty. “A Ph.D. program not only doesn’t subtract from the undergraduate experience,” Friedberg said, “it deeply adds to it, and builds BC’s international intellectual prominence.”
Persuaded, the University authorized the new program, and the math department began hiring bright young faculty members. Today, the department is broadly understood to include a third area of focus, algebraic geometry, which was broken out from the number theory group. About a third of math department undergrads now pursue the BS degree.
“Sol Friedberg and his colleagues were able to do a number of things over those first few years,” Quigley said. “They launched the Ph.D. program, of course, but I’d say even more important, they hired just a terrific cohort of younger faculty, some of whom Lisa Piccirillo worked with.” Among those hires, in fact, were Grigsby and Greene.
AFTER GRADUATING IN 2013, Piccirillo chose to pursue her Ph.D. at the University of Texas because of the university’s excellent topology program and its reputation as a great place for female grad students in math. In 2014, just 29 percent of math and science Ph.D.s were awarded to women, according to the National Science Foundation, but at Texas, something like 40 percent of graduate math students were women.
By and large, Piccirillo felt welcomed and encouraged as a female mathematician. “But now and again, things happen,” she told me. “For example, in grad school, I would receive notes in my department mailbox commenting on my appearance.”
Overall, Piccirillo excelled during her six years at the University of Texas, finding both strong mentorship and a supportive research community. The time coincided with her deepening connection to the math itself. She loved to turn problems over in her mind, thinking about how one higher-dimension shape might be manipulated to resemble an entirely different one. It was thrilling, creative work, as much about aesthetic as arriving at a particular result. “When you perform a calculation, sometimes there’s really clever tricks you can use or some ways that you can be an actual human and not a computer in the performing of the calculation,” Piccirillo says. “But when you make a logical argument—that’s entirely yours.”
Outside of her studies, Piccirillo liked to make beautiful things. “You walked into her house,” recalled James Farre, a friend from the University of Texas who is currently a postdoc at Yale, “and the feel was airy and beachy, rustic, but almost austere—like you were in a museum with things like dried flowers that she had handpicked and tied in a string. All kinds of beautiful prints that she had made and maps that she had collected. She has a very, very strong sense of aesthetic. I think that this is not completely atypical. Math that people like is often thought of and talked about as beautiful or deep.” Piccirillo carved wooden spoons for a while, and made large-scale wood-cut prints of fish and vegetables. She and her roommate, Wiley Jennings, built a dining room table together. For a time, she was obsessed with buying and repairing vintage Japanese motorcycles.
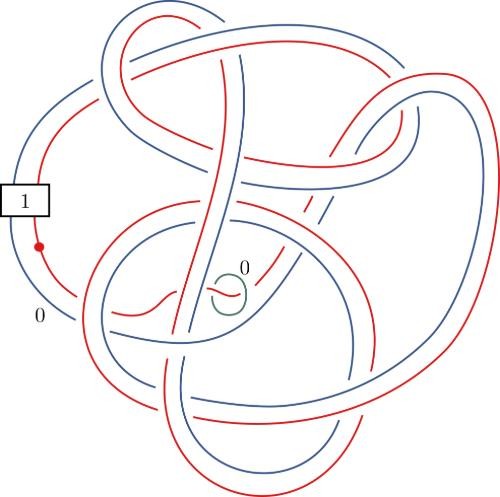
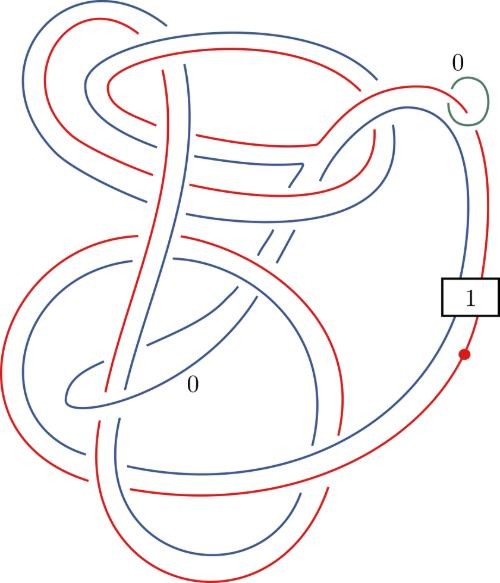
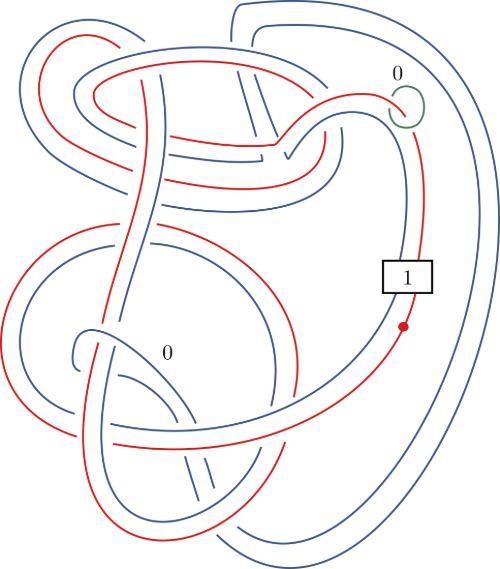
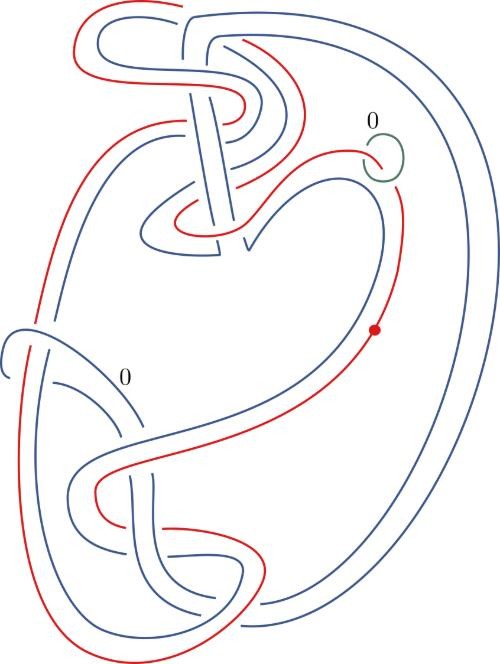
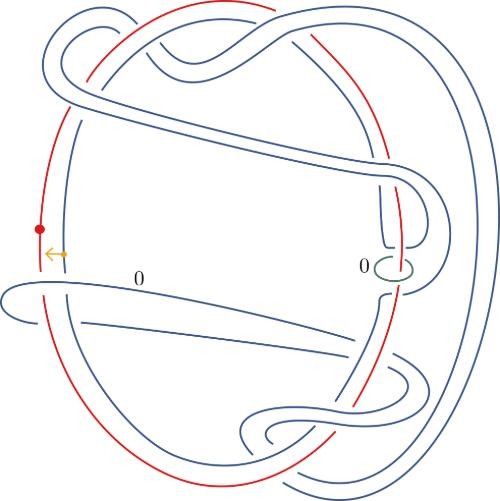
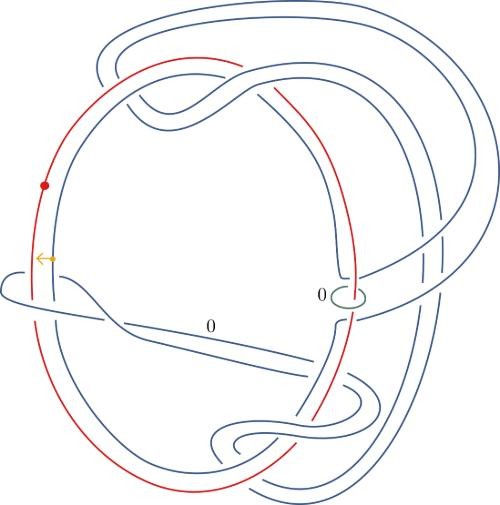
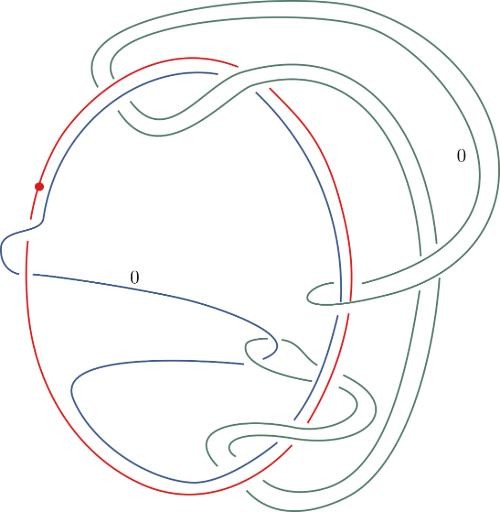
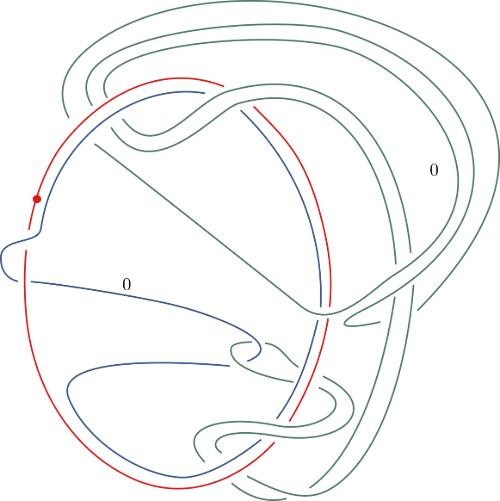
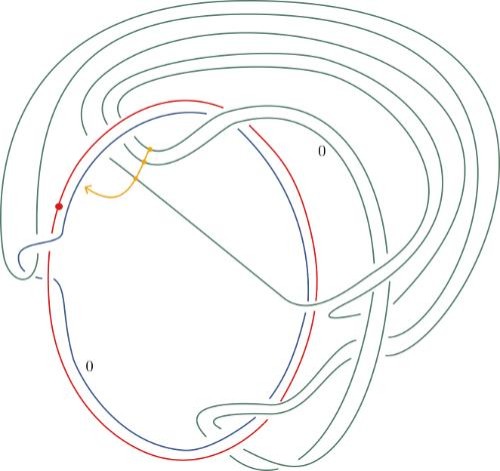
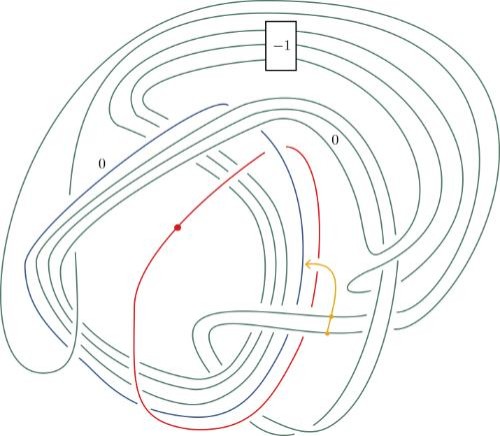
THE DAY AFTER HEARING about the Conway knot problem, Piccirillo, then 27, sat down at her desk and began looking for a solution. Because much of her graduate work involved building pairs of knots that were different but shared some 4D properties, she already knew that any two knots that share the same 4D space also share sliceness—they’re either both slice or both not slice. Since her goal was to prove that the Conway knot wasn’t slice, her first step was to come up with an entirely different knot with the same four-dimensional space, she explained. “Then I’ll try to show that the other knot isn’t slice.”
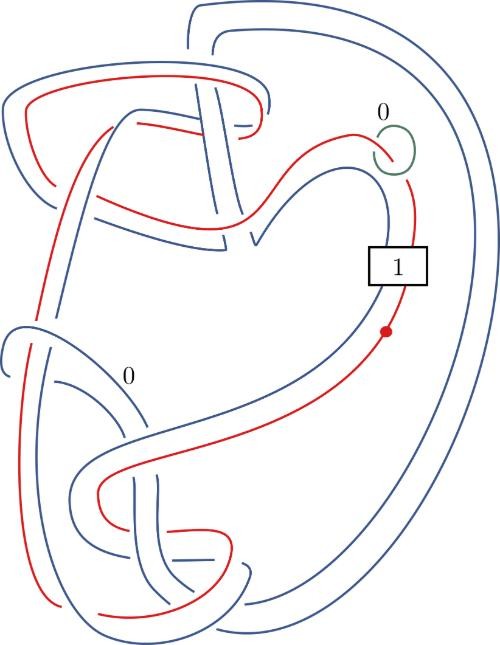
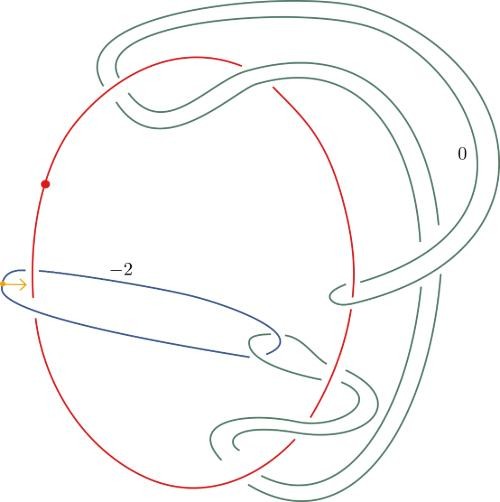
Over the next several days, she hand-sketched her knot, then, in an attempt to prove that it was not slice, she would feed it into a computer, “and based on the data of the knot, maybe based on how its crossings look or other data that you can pull from the knot, the algorithm spits out an integer.” In less than a week, Piccirillo had built a knot that hit the sweet spot: It had the same 4D properties as Conway’s knot, and it was found by the algorithm to be not slice.
She had suddenly succeeded where countless mathematicians had failed for five decades. She had solved the Conway knot problem.
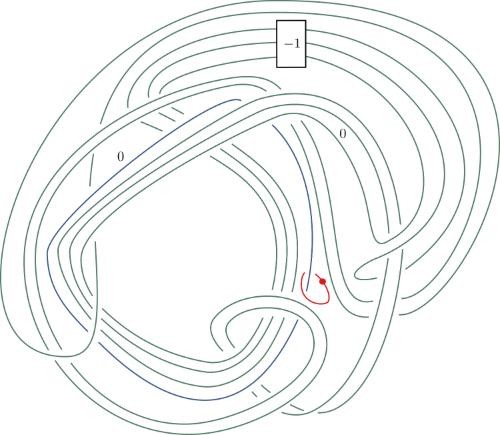
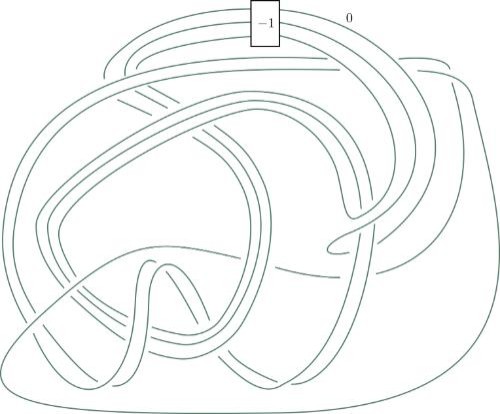
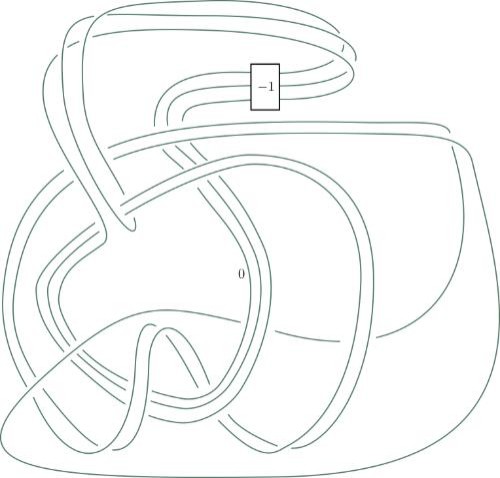
This sequence of knot sketches is one of the two steps Piccirillo used to solve a problem that had stumped mathematicians for decades.
NOT LONG AFTER THE BREAKTHROUGH, Piccirillo attended a meeting with the University of Texas math Professor Cameron Gordon. When she mentioned her solution, Gordon was skeptical. He asked Piccirillo to walk him through the steps. “Then he made me write it down, like all up on the board,” she told me, “and then he got very excited and started yelling.”
Piccirillo submitted her solution to the Annals of Mathematics, and the prestigious math journal agreed to publish her paper. When I asked James Farre, the Yale postdoc, to explain the significance of having a paper published in the Annals, he laughed for several seconds. “It’s head and shoulders the most important and influential journal in mathematics,” he says. “That’s why I’m laughing. It’s amazing and it’s so cool!”
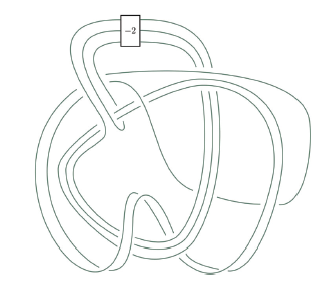
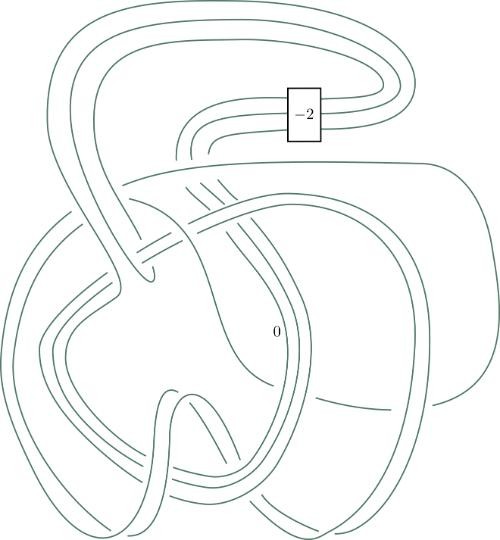
This knot, created by Piccirillo, finally solved the famous Conway knot problem.
By the time Piccirillo’s paper appeared in the journal about a year later, word of her solution had already spread throughout the math world. After graduating from UT in 2019, she started her postdoctoral work at Brandeis. “The last time I saw her was in January,” said Wiley Jennings, her roommate in Austin, who recently completed a Ph.D. at Stanford. “She was out at a faculty visit here at Stanford. To be invited, as someone who has done one year or less [of postdoc study]—just finished their Ph.D., essentially—I mean, that’s insane. It’s unheard of.”
Postdoc positions typically run for three or four years, but Piccirillo found herself in high demand. In July, she started a new tenure-track position as an assistant professor at MIT. It’s been a whirlwind, and I wondered how her life has changed. She acknowledged that there sometimes is a feeling of pressure, based on what she’s already accomplished. In practice, math is about trying to prove simple statements and failing—basically all of the time, for everyone. “So,” she said, “I’m having to relearn how to be okay with the fact that most of the time I’m failing to prove really simple stuff when I’m feeling the weight of these expectations.”
When I asked about her goals, Piccirillo said one of her priorities is to help grow and broaden the mathematics community. “There certainly are many young women, people of color, non-heterosexual or non-gender-binary people who feel put at an arm’s length by the institution of mathematics,” she said. “It’s really important to me to help mitigate that in any small ways I can.” One important way to do that, she continues, is to help shatter the myth of the math prodigy.
When universities organize math conferences, she said, they should avoid inviting speakers who “give talks where they go really fast and they try to show you how smart they are and how hard their research is. That’s not good for anyone, but it’s especially not good for young people or people who are feeling maybe like they don’t belong here.” What those people in the audience don’t know, she said, is that nobody else really understands it either.
“You don’t have to be really ‘smart’—whatever that means—to be a successful mathematician,” Piccirillo said. “There’s this idea that mathematicians are geniuses. A lot of them seem to be child prodigies that do these Olympiads. In fact, you don’t have to come from that background at all to be very good at math, and most mathematicians, including many of the really great ones, don’t come from that sort of background.”
Some of them even go on to produce work that alters the course of mathematics.
Chalk illustrations by Catherine Owens


 print
print mail
mail